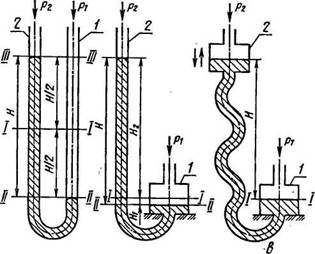
Принцип действия жидкостных манометров можно проиллюстриро­вать на примере U-образного жидкостного манометра (рис. 4, а), состоя­щего из двух соединенных между собой вертикальных трубок 1 и 2,

п                 (Г

Рис. 4. Основные типы жидкостных манометров

наполовину заполненных жидкостью. В соответствии с законами гидро­статики при равенстве давлений pi ир2 свободные поверхности жидкос­ти (мениски) в обеих трубках установятся на уровне I—I. Если одно из давлений превышает другое (pi > p2), то разность давлений вызовет опускание уровня жидкости в трубке 1 и, соответственно, подъем в труб­ке 2, вплоть до достижения состояния равновесия. При этом на уровне II—П уравнение равновесия примет вид

Др=р, -р2=#- р —g,                (2.1)

т. е. разность давлений определяется давлением столба жидкости высо­той Н с плотностью р.

Уравнение (1.6) с точки зрения измерения давления является фун­даментальным, так как давление, в конечном итоге, определяется основ­ными физическими величинами — массой, длиной и временем. Это урав­нение справедливо для всех без исключения типов жидкостных маномет­ров. Отсюда следует определение, что жидкостный манометр — мано­метр, в котором измеряемое давление уравновешивается давлением столба жидкости, образующегося под действием этого давления. Важно подчеркнуть, что мерой давления в жидкостных манометрах является

высота стол а жидкости, менно это обстоятельство привело к появле­нию единиц измерений давления мм вод. ст., мм рт. ст. и других которые естественным образом вытекают из принципа действия жид­костных манометров.

Чашечный жидкостный манометр (рис. 4, б) состоит из соединенных между собой чашки 1 и вертикальной трубки 2, причем площадь попереч­ного сечения чашки существенно больше, чем трубки. Поэтому под воз­действием разности давлений Ар изменение уровня жидкости в чашке гораздо меньше, чем подъем уровня жидкости в трубке: Hi = H2 • f/F, где Их — изменение уровня жидкости в чашке; Н2 — изменение уровня жидкости в трубке; / — площадь сечения трубки; F — площадь сечения чашки.

Отсюда высота столба жидкости, уравновешивающей измеряемое давление Н — Hi + #2
= #2 (1 + f/F), а измеряемая разность давлений

р, — р2 = #2 ‘ Р • #(1 +//*) —       (2-2)

Поэтому при известном коэффициенте к = Г + f/F разность давлений может быть определена по изменению уровня жидкости в одной трубке, что упрощает процесс измерений.

Двухчашечный манометр (рис. 4, в) состоит из двух соединенных при помощи гибкого шланга чашек 1 и 2, одна из которых жестко за­креплена, а вторая может перемещаться в вертикальном направлении. При равенстве давлений pi и р2 чашки, а следовательно, свободные по­верхности жидкости находятся на одном уровне I—I. Если Pi > р2, то чашка 2 поднимается вплоть до достижения равновесия в соответствии с уравнением (2.1).

Единство принципа действия жидкостных манометров всех типов обусловливает их универсальность с точки зрения возможности изме­рения давления любого вида — абсолютного и избыточного и разности давлений.

Абсолютное давление будет измерено, если р2
= 0, т. е. когда прос­транство над уровнем жидкости в трубке 2 откачано. Тогда столб жид­кости в манометре будет уравновешивать абсолютное давление в трубке 4т.е.рабс=Я*р —g.

При измерении избыточного давления одна из трубок сообщается с атмосферным давлением, например, р2 = Рагм. Если при этом абсолют­ное давление в трубке 1 больше чем атмосферное давление (р% >ратм)> то в соответствии с (1.6) столб жидкости в трубке 2 уравновесит избы­точное давление в трубке 1}т. е. ри = # • р • g: Если, наоборот, pi <Рам» то столб жидкости в трубке 1 будет мерой отрицательного избыточного давления ри = —Н • р • g.

При измерении разности двух давлений, каждое из которых не равно атмосферному давлению, уравнение измерений имеет вид Др = pi — Рг = = Н • р ‘ g Так же, как и в предыдущем случае, разность может прини­мать как положительные, так и отрицательные значения.

К важной метрологической характеристике средств измерения дав­ления   относится   чувствительность   измерительной  системы,  которая

во многом определяет точность отсчета при измерениях и инерционность. Для манометрических приборов под чувствительностью понимается от­ношение изменения показаний прибора к вызвавшему его изменению давления (и = АН/Ар). В общем случае, когда чувствительность непосто­янна в диапазоне измерений

п = ton -^ при Ар -* 0,            (2.3)

где АН — изменение показаний жидкостного манометра; Ар — соответ­ствующее изменение давления.

Принимая во внимание уравнения измерений, получим: чувствительность U- образного или двухчашечного манометра (см. рис. 4, аи 4, в)

"-—р.                                   (2.4,*)

чувствительность чашечного манометра (см. рис. 4, б)

Как правило, для чашечных манометров F »/, поэтому уменьше­ние их чувствительности по сравнению с U- образными манометрами незначительно.

Из уравнений (2.4, а) и (2.4, б) следует, что чувствительность цели­ком определяется плотностью жидкости р, заполняющей измерительную систему прибора. Но, с другой стороны, значение плотности жидкости со­гласно (J.6) определяет диапазон измерений манометра: чем она больше, тем больше верхний предел измерений. Таким образом, относительное значение погрешности отсчета от значения плотности не зависит. Поэтому для увеличения чувствительности, а следовательно, и точности, разрабо­тано большое количество отсчетных устройств, основанных на различных принципах действия, начиная от фиксации положения уровня жидкости относительно шкапы манометра на глаз (погрешность отсчета около 1 мм) и кончая применением точнейших интерференционных методов (погрешность отсчета 0,1-0,2 мкм). С некоторыми из этих методов можно познакомиться ниже.

Диапазоны измерений жидкостных манометров в соответствии с (1.6) определяются высотой столба жидкости, т. е. размерами маномет­ра и плотностью жидкости. Наиболее тяжелой жидкостью в настоящее время является ртуть, плотность-которой р = 1,35951 • 104 кг/м3. Столб ртути высотой 1 м развивает давление около 136 кПа, т. е. давле­ние, не на много превышающее атмосферное давление. Поэтому при из­мерении давлений порядка 1 МПа размеры манометра по высоте соизме­римы с высотой трехэтажного дома, что представляет существенные экс­плуатационные неудобства, не говоря о чрезмерной громоздкости кон­струкции. Тем не менее, попытки создания сверхвысоких ртутных ма­нометров предпринимались. Мировой рекорд был установлен в Париже,

где на базе конструкций знаменитой Эйфелевой башни был смонтирован манометр высотой ртутного столба около 250 м, что соответствует 34 МПа. В настоящее время этот манометр разобран в связи с его бес­перспективностью. Однако в строю действующих продолжает оставаться уникальный по своим метрологическим характеристикам ртутный мано­метр Физико-технического института ФРГ. Этот манометр, смонтирован­ный в 10-этажной башне, имеет верхний предел измерений 10 МПа с по­грешностью менее 0,005 %. Подавляющее большинство ртутных мано­метров имеют верхние пределы порядка 120 кПа и лишь изредка до 350 кПа. При измерении относительно небольших давлений (до 10-20 кПа) измерительная система жидкостных манометров заполняется водой, спиртом и другими легкими жидкостями. При этом диапазоны измерений обычно составляют до 1-2,5 кПа (микроманометры). Для еще более низких давлений разработаны способы увеличения чувстви­тельности без применения сложных отсчетных устройств.

Микроманометр (рис. 5), состоит из чашки /, которая соединена с трубкой 2, установленной под углом а к горизонтальному уровню

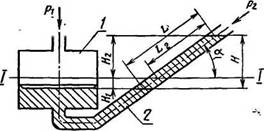
Рис. 5- Чашечный микроманометр с наклонной труб­кой

I-I. Если при равенстве давлений р, и р2
поверхности жидкости в чашке и трубке находились на уровне I-I, то увеличение давления в чашке (Pi > Рг) вызовет опускание уровня жидкости в чашке и ее подъем в трубке. При этом высота столба жидкости Н2 и его длина по оси труб­ки L2 будут связаны соотношением Я2 = L2 sin a.

Учитывая уравнение неразрывности жидкости Н, F = L2 • /, нетруд­но получить уравнение измерений микроманометра

Pi ~Рг -H’P -g = L2 ‘p ‘g (sina + —),      (2.5)

где L2 — перемещение уровня жидкости в трубке вдоль ее оси; а — угол наклона трубки к горизонтали; остальные обозначения прежние.

Из уравнения (2.5) следует, что при sin a « 1 h//F« 1 перемеще­ние уровня жидкости в трубке во много раз превысит высоту столба жидкости, необходимую для уравновешивания измеряемого давления.

Чувствительность микроманометра с наклонной трубкой в соответ­ствии с (2.5)

п = -^- =—— 1——— .                   (2.6)

Ар      р- g (sin a +//F)

Как видно из (2.6), максимальная чувствительность микроманомет­ра при горизонтальном расположении трубки (а = О)

F    #      1 "max~   /      "" P-g ‘

т. е. в отношении площадей чашки и трубки больше, чем у U- образного манометра.

Второй способ увеличения чувствительности состоит в уравновеши­вании давления столбом двух несмешивающихся жидкостей. Двухчашеч-ный манометр (рис. 6) заполняется жидкостями так, чтобы граница их

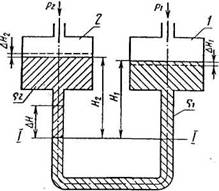
Рис. 6. Двухчашечный микроманометр с двумя жидкостями (р, >р2)

раздела находилась в пределах вертикального участка трубки, примыка­ющей к чашке 2. Прир! = р2 давление на уровне I—I

Я, pi =H2 9г (Pi

Тогда при повышении давления в чашке 1 уравнение равновесия бу­дет иметь вид

&P=Pi -Рг =АЯ[(Р1
-р2) +//F0»! +р2)] g,   (2.7)

где рл  — плотность жидкости в чашке 1; р2
— плотность жидкости в чашке 2

Кажущаяся плотность столба двух жидкостей

‘      Рк = (Pi — Рг) +//F (Pi + Рг) •  (2.8)

Если плотности Pi и р2 имеют близкие друг другу значения, af/F«. 1, то кажущаяся или эффективная плотность может быть снижена до вели­чины pmin =//F(Pl + p2) а 2рх f/F.

При этом, соответственно, увеличивается чувствительность

н = ^-= 1— ,                           (2.9)

ДР      Рк-8

где рк — кажущаяся плотность в соответствии с (2.8).

Так же, как и ранее, увеличение чувствительности указанными спо­собами автоматически уменьшает диапазоны измерений жидкостного манометра, что ограничивает их применение областью микроманометрии. Учитывая также большую чувствительность рассматриваемых способов к влиянию температуры при точных измерениях, как правило, находят применение способы, основанные на точных измерениях высоты столба жидкости, хотя это и усложняет конструкции жидкостных манометров.